|
|
|
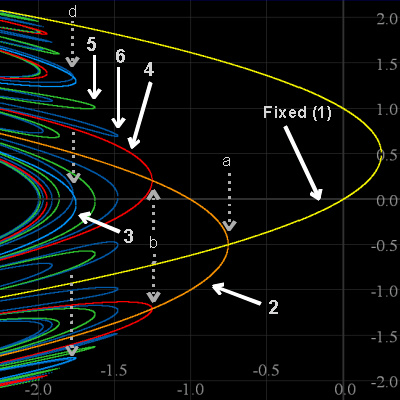
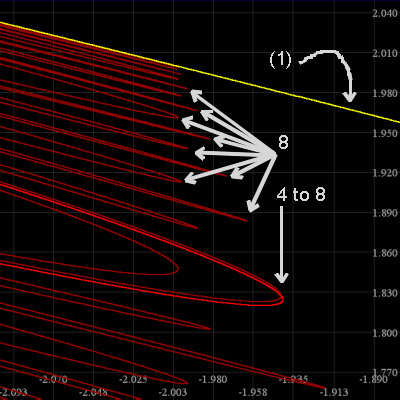
| This is the same image as on the previous page. In all pictures on this page the coloring scheme remains the same: points of a given prime period are colored identically from picture to picture. | Above, we've "zoomed in" to the upper left-hand quarter of the first picture, labeling a few more curves according to periodicity. The vertical arrows are on c values at which new periodic cycles are born, at both period doubling bifurcations (PDBs) and saddle node bifurcations (SNBs). 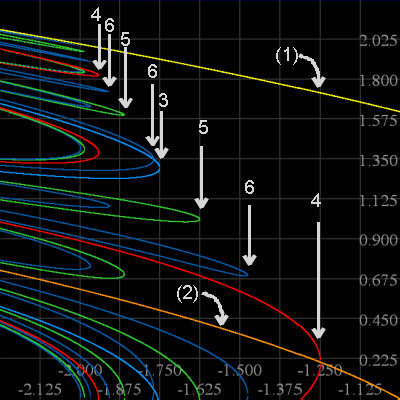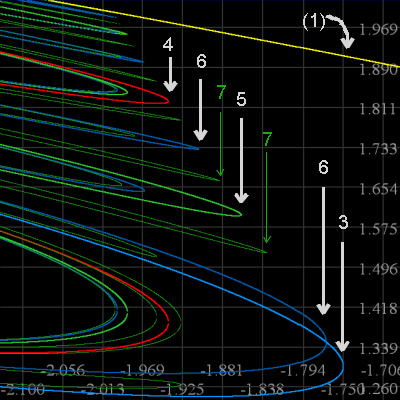| Now a zoom into the upper left quarter of the middle picture. We've also introduced points of prime period 7. Note this can't be all of them, by Sarkovskii's theorem. There are in fact two other pairs of 7-cycles present, but too far "south" to show up in this picture. And both are "born" to the right of the birth of the 3-cycle. Altogether there are nine saddle node bifurcations in fc7; seven of them are present in this figure, and two are labeled. |
|
|
|
|
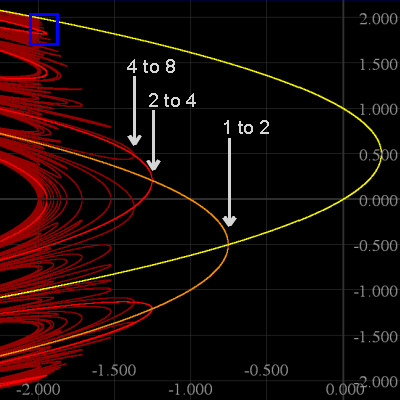
Above we only show points whose periods divide 8. In particular we see the c values at which fc undergoes the period doubling bifurcations (PDBs) from 1 to 2, 2 to 4 and 4 to 8, as c
decreases from right to left across the picture. This "period doubling scenario" continues forever (ie, 8 to 16, 16 to 32, 32 to 64, etc) and does it all before c reaches FIND THAT POINT.
Another scenario beginning 4 to 8, 8 to 16, 16 to 32..., starts with 4 to 8 near c=-1.9415, but you can't see it in this picture because of the required resolution. The middle picture is a zoom into the blue box; the 4 to 8 PDB becomes easier to see. |
Above, we've "zoomed in" to the blue box seen in the left-hand picture. In addition to the period 8 cycle "born" through period doubling, several different pairs of period eight cycles arising through saddle node bifurcations (SNBs) are also labeled, but altogether there are fifteen pairs of prime period 8 cycles born through SNBs. |
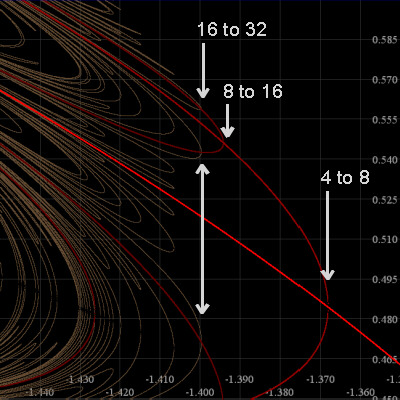
Above we've zoomed in to show the PDBs from 8 to 16 and 16 to 32. Note also the incredible number of points of prime period 32 "born" through SNBs. There is another period doubling scenerio starting with 16 to 32 in this picture; can you find it? Hint: use the colors.
Note this picture shows only points whose periods divide 32. The left half becomes incomprehensively crowded if we try to show all points of period less than 32. |
|
Return to Chip's Home Page
Return to Bifurcation and Orbit Diagrams page (one level up) |
© 2004 by Chip Ross Associate Professor of Mathematics Bates College Lewiston, ME 04240 |