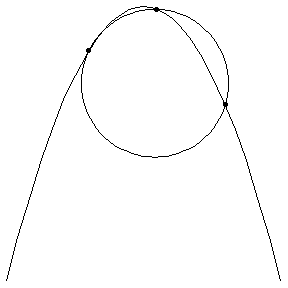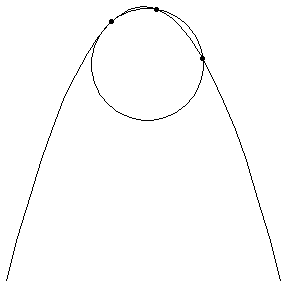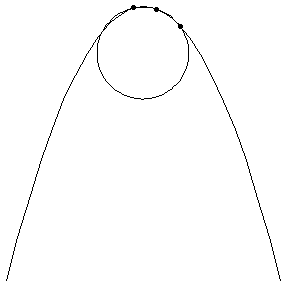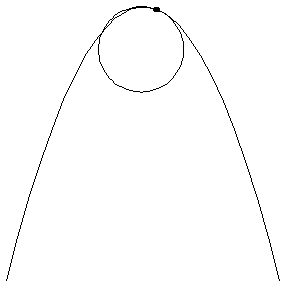
| On curved tracks, there are additional forces on a coaster to keep the coaster on the track. This additional force is proportional to the curvature, which is the recriprocal of the tangent circle's radius. The following GIFs help to visualize these tangent circles. |
| The first three GIFs show how the tangent circle is formed, using three points and a limit. | ||
Loop 'de Loop
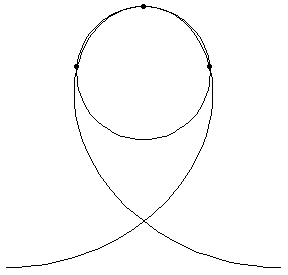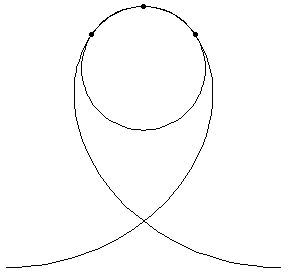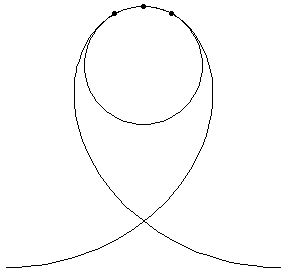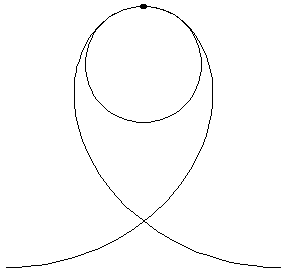
|
Parabola
|
Sine curve

|
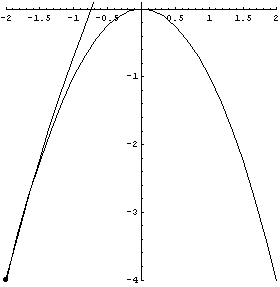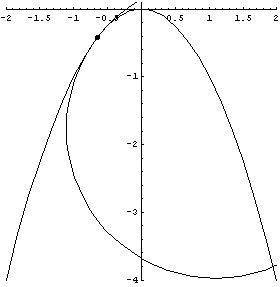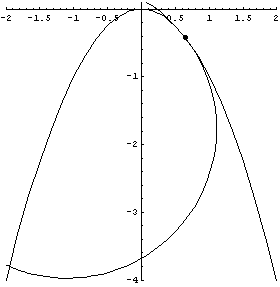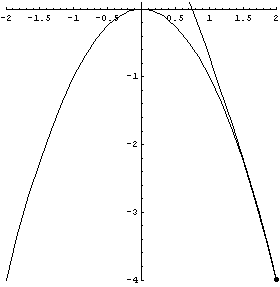
| The next two GIFs show the tangent circles moving around a track. | |
Loop 'de Loop
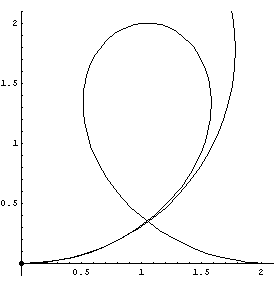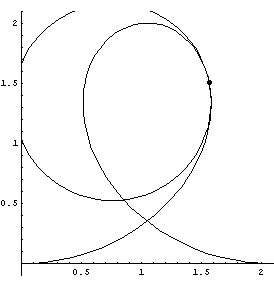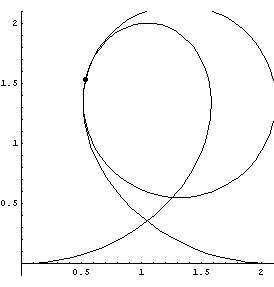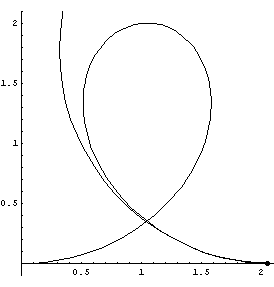
|
Parabola
|