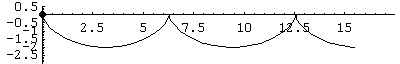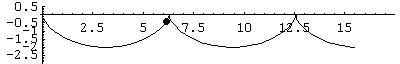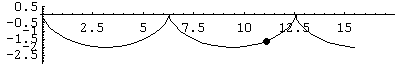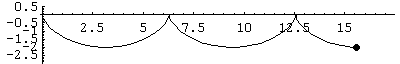|
One simple way to model the motion of a roller coaster is to assume there is no friction, and that
nothing rolls. This is analogous to thinking of a bead moving down a wire fixed in space.
|
We start with something simple: a straight line.
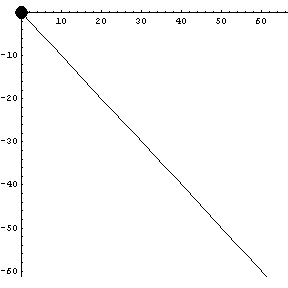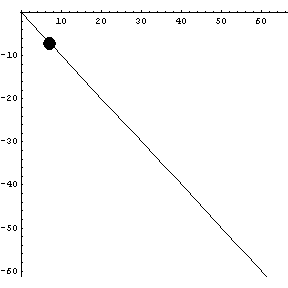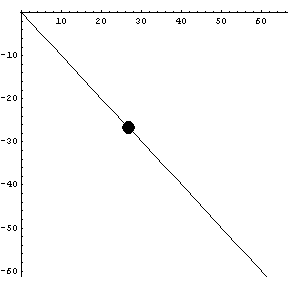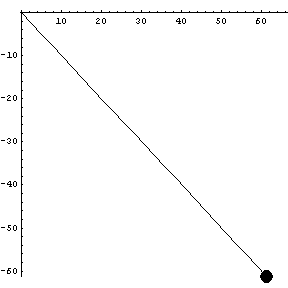
|
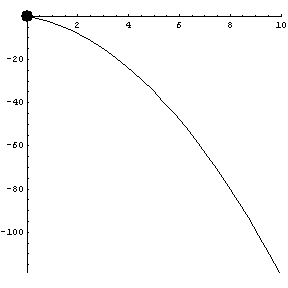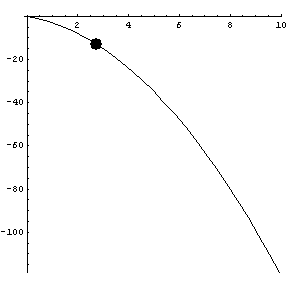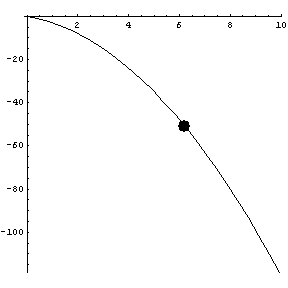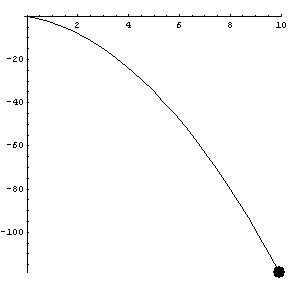
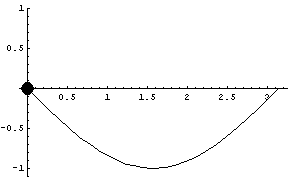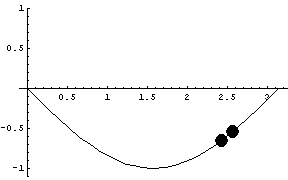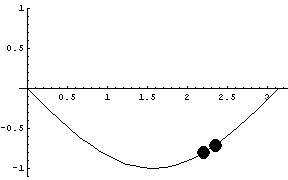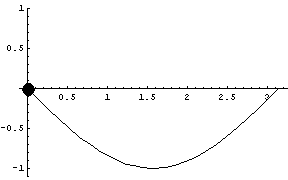
A parabola: note the axes are not to scale.
|
Getting a little more fancy, here's a cycloid.
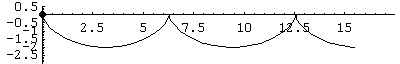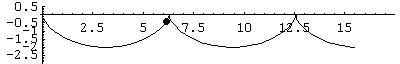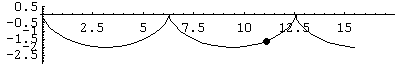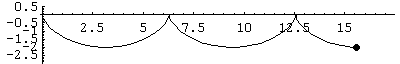
|
Joining two curves together, we have a Loop 'de Loop.
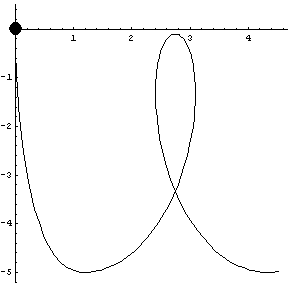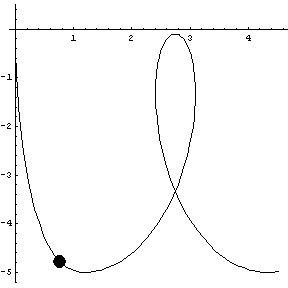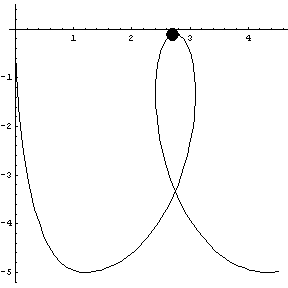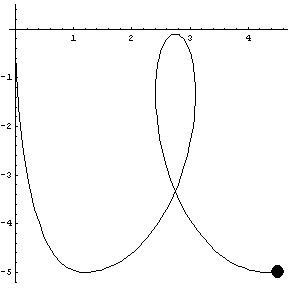
|
|
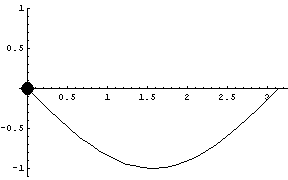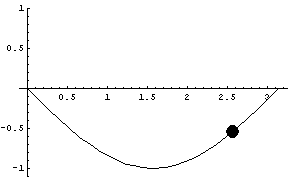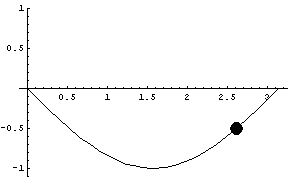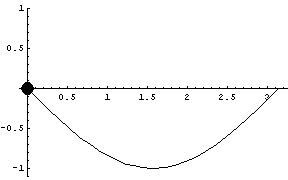
Next we show a negative sine curve, computed two ways:
|
1.) with position as a function of time
|
2.) using the Hamiltonian method
|
The following graphic shows both sine approximations simultaneously
|
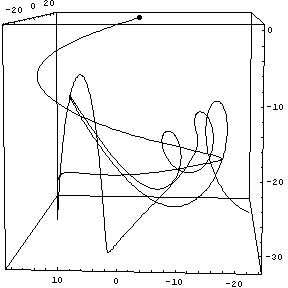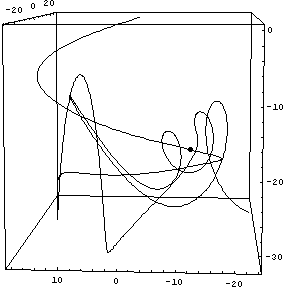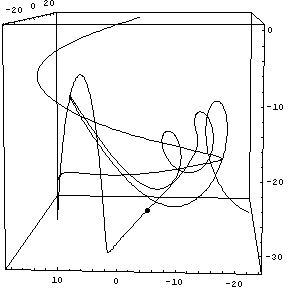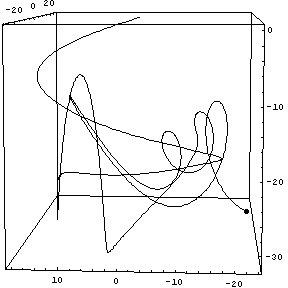
As a finale, here's a 3-D track.
|