Repelling Points on Julia Sets

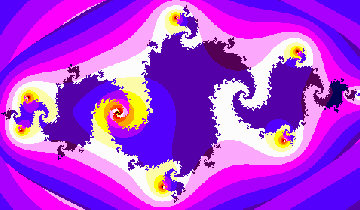
For a polynomial such as f(z)=z^2+C where z and C are complex numbers, the Julia Set corresponding to this value of C may be defined as the (closure of) the set of all repelling periodic points. For the image on the left, we can visualize the Julia set set because it is also the boundary between the points which escape to infinity (colored using reds/oranges/yellows) and those which get attracted to the attracting two-cycle. (This 2-cycle contains the two points M and N labeled in the figure. Here f(M)=N and f(N)=M and all the points whose orbits are attracted to this cycle are colored with blues/purples, etc.) The image in the upper left shows this boundary more clearly.

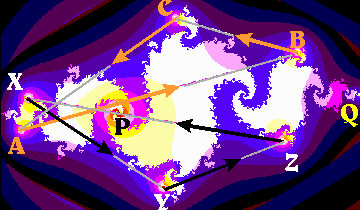
Now, traditionally repelling periodic points are hard for a computer to find. Unless the computer can store the coordinates of such a point precisely, the calculated orbit moves away from the true orbit of the repelling point. For the picture on the right, we have located the 6 points of period 3 and the two fixed points as follows: We ask the computer to ONLY calculate the first three members of the orbits of each point on the screen, and assign a color to each such point based on how far away from it its third iterate is. "Bullseyes" naturally form around points of period 3 (and since the fixed points are also period 3, they show up as well).

In the image below, left, we've labeled the eight points: A,B,C and X,Y,Z form two cycles of prime period 3, and P and Q are the two fixed points for this Julia set. All eight points lie on the Julia set, and all 8 are repelling. Together with the points M and N in our top image, we therefore, we know the locations of all the points of period 1, 2, and 3. 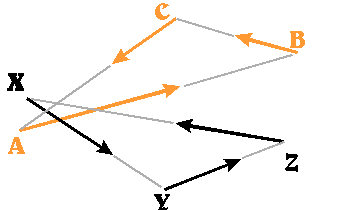(Technical reminder: there can be only two points of prime period 2) The right-hand picture shows just the two 3-cycles.

Details:

Theses images were produced by an old-fashioned DOS program I wrote in Turbo/Borland Pascal, "screen-captured", and subsequently labeled using the Corel Print&Photo House programs.