Prof.Chip Ross: Bifurcation and Orbit Diagrams

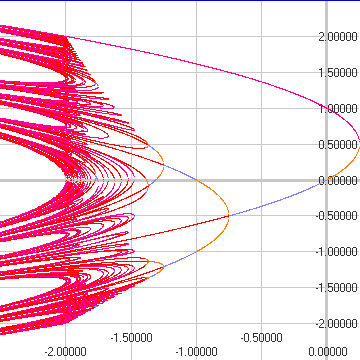
On the left is the bifurcation diagram. It shows for each C value on the horizontal axis, the locations on the vertical axis of any points of periods 1 through 8. For a fixed C value, points of period N are found by scanning the (vertical) interval [-2.5,2.5] for crossings of the line y=x and the f'n f_C(x)=x^2+C composed with itself N times --- this algorithm is detailed in our paper. The slope of (f_C)^N at such a crossing determines if the point is on an attracting or repelling cycle. The above bifurcation diagram is colored according to these slopes:

MAGENTA: the slope is greater than 1; the point is on a REPELLING cycle
ORANGE: the slope is between 0 and 1; the point is on an ATTRACTING cycle
BLUE: the slope is between -1 and 0; the point is on an ATTRACTING cycle
RED: the slope is less than -1; the point is on a REPELLING cycle

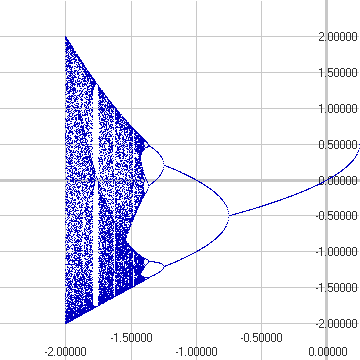
The points colored orange and blue in the bifurcation diagram also appear in the orbit diagram, the figure on the right. This figure is produced as follows: For each C value on the horizontal axis, hundreds of members of the orbit of 0 are calculated, but only the last few are plotted, in hopes that by then the orbit has been attracted to a periodic cycle, if indeed there is an attracting one for that C value. Otherwise, the orbit of 0 bounces around chaotically, (or "escapes to infinity", in which case no points are shown because the members of the orbit have become very large. For C<-2 this is the case).

The two diagrams coincide at C values for which there is a attracting periodic cycle; again such points appear orange and blue in the bifurcation diagram

Details The above pictures were drawn with my Windows version of "orbits", saved to bitmap files, and subsequently compressed using Microsoft's "Picture It" photo editing program.

Return to Chip's Home Page
Return to CMJ Article Page