Cauliflower

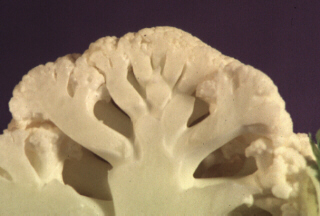
One of the properties of fractals is that they contain no information that gives you a sense of scale: little pieces of a fractal look like the whole thing, and in particular, if someone shows you a zoom in to a fractal, you can't tell if they've zoomed in by a factor of 10 or 10 million! Now, Nature's best fractals have this "detail in the detail" property for only a finite number of repetitions, and the cauliflower is one of the best examples. Its surface is made of big bumps. On the big bumps are smaller bumps, and on those, still smaller bumps, and so on. It's easy to visualize each big bump as a whole cauliflower in its own right. Indeed, although the right-hand picture is a zoom into the one on the left, it's not too hard to imagine that you are looking at a whole pile of cauliflowers on display at your local supermarket.

Side View

The Cauliflower Family

Yes, there's the big daddy on the right, smaller mom on the left and the little kids in front --- looks like four different sized cauliflowers, right? But these are all pieces of the same single cauliflower. The point is, when you break off a piece of a fractal, it looks again like the whole fractal, just smaller.

Details: I produced these pictures for the Science and Math Academies for Maine K-12 teachers (more about the Academies can be found at other places in this document). For teachers who are interested in teaching fractals to their students, I wanted to emphasize (1) that fractals are found all around us, and (2) it's possible to create displays about them without expensive materials. Using a 35mm camera on a tripod, I took these pictures for the "slide show" portion of my week with the Academy teachers. Arranged on dark blue construction paper, the cauliflower was photographed using incandescant lighting, and a blue filter to compensate for excess amount of red light produced by regular household lightbulbs...