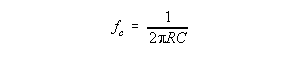
Introduction
In this experiment you will build several types of
passive filters,
including high pass, low pass, and bandpass filters, and determine their
frequency transmission characteristics.
Apparatus
breadboard
capacitor
SR 760 FFT spectrum analyzer
oscilloscope
resistors (1k,0.1k) DS
345 function generator (FG)
BNC cables
inductor
digital multimeter
Procedure
The breadboard is a device that enables you to use pieces of
wire to quickly create electronic circuits, which can then be tested. Take
a moment to check out your breadboard and ask the instructor if you're
not sure about how it works. Please note that for this experiment, we
don't want to plug the breadboard power cord into the wall socket. This
is so that its "ground" will be "floating," i.e. not "tied" to "Earth ground."
Note
that your coaxial cables have been connected. In this experiment you'll
place wires and circuit elements on the breadboard in order to build filters;
you'll use the FG to generate electronic waves and the spectrum analyzer
and oscilloscope will be used to measure the output of the filters you
construct.
1. Getting started
Turn on the equipment, and set the FG to generate a 1 kHz sine wave,
with an amplitude of 0.2 Volt. Observe this output on your spectrum analyzer
(SA) by plugging its coaxial cable directly into the SA. Set the display
of the SA to be "linear," by pressing the "meas" keypad, then the "display"
submenu, and set this to "linear." Observing the SA, note the frequency
and amplitude of the peak corresponding to 1 kHz by using the "marker"
knob. Does the SA display make sense? Be sure to check with the instructor
if it does not.
2. RC Filter
Measure the resistance of your nominal 1 k resistor using a multimeter.
Then connect this resistor and the brown disk-shaped capacitor in series
to construct an RC filter as described in class. Sketch a schematic of
the circuit and set-up in your lab notebook. Drive the input with your
1 kHz, 0.2 V wave, and observe the output voltage across the resistor
with
the SA. Set the "step" of the FG to 1 kHz, and tune upwards from 1 kHz
using the up arrow key...what do you observe? Does it make sense?
Now set up to take a spectrum, in the same way we did the frequency response of the loudspeaker. Use the "linear" scan of the FG, with a start frequency of 0 Hz and a stop frequency of 6000 Hz. Remember, to set the stop frequency you press "shift" then "start," and then enter "6000" and press the "Hz" key. You can check the "span (depth)" to ensure that it's at 6000 Hz. The scan rate should be 0.01 Hz, as before. Recall this corresponds to a time of 100 seconds, which requires about 6300 signal averages from the SA. Press the SA "Freq" key and set the "start frequency" to 0 Hz, and the "span" to 6.25 kHz, to match the range of your scanning FG. Press the "sweep on/off" key as you press the "start" key to begin the SA averaging, and record your spectrum. Use the "autoscale" key to scale the plot on the screen.
After your spectrum has been completed, move the "marker" to the highest voltage value on the spectrum and record it in your lab notebook. Calculate the cutoff voltage, which should be 0.707 times this peak voltage. Now move the "marker" down the spectral curve until you reach this cutoff voltage, and record the cutoff frequency. Save the data on the computer and plot the spectrum.
Question 1. What type of filter is this, high pass or low pass?
Question 2. If the input is a sine wave at the cutoff frequency with an amplitude of 1 Volt, what do you expect the output amplitude to be?
3. RL Filter
Now build a circuit with the same resistor in series with the inductor,
a relatively large gray box-shaped circuit element. Sketch the circuit
schematic in your lab notebook. As before, drive it with your sine wave
and measure the output across the resistor. Scan the frequency, and record
a spectrum as before, but this time adjust the FG to scan from 0 Hz 3000
Hz, and set the SA to start at 0 Hz on the 3.125 kHz span setting.
Note that you may have a "noise" spike at the lowest frequencies, which
is to be avoided. Move the marker to the base of this spike and measure
the highest voltage. Calculate 0.707 times this value, move the marker
to the cutoff voltage to find the cutoff frequency, and record it.
Again, import the data to the computer and make a hard copy of the spectrum.
Question 3. What type of filter is this?
4. Series LC circuit.
Keeping your circuit from part 3. above, now connect the capacitor
in series with the inductor, and put the 100 Ohm resistor
in parallel with the 1 kilo Ohm resistor. Take a spectrum with the SA as
before, using the same parameters as you did for the inductor. Use the
marker to measure the resonance frequency in Hz and import the data
to the computer to make a hard copy.
Question 4. What do you observe at the resonant frequency? Can you explain what's happening?
Analysis
1. Using the expression for the cutoff frequency:
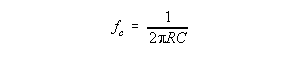
2. Using the expression for the cutoff frequency:
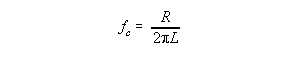
3. Now compare the experimental value of the resonance frequency in the parallel RC to the theoretical value:
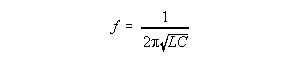
Question 5. How well do your experimental and theoretical values for the resonance frequency agree? Comment on possible sources of error. If the agreement is not good, why not?
Question 6. Describe how each of these filters could be used in a loudspeaker system.