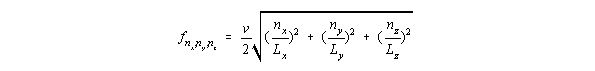
Introduction
In this experiment, you'll investigate sound wave resonances in a three dimensional cavity, which simulates a very small listening room. For a rectangular box with sides of length L_x, L_y, and L_z, the resonance frequencies are given by:

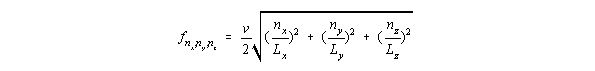
where v is the speed of sound in the cavity, and n_x, n_y, and n_z are the number of pressure nodes in the standing wave along the x, y, and z dimensions, respectively.

Apparatus

• Stanford Research DS345 synthesized function generator (FG)
• Stanford Research SR760 FFT spectrum analyzer (SA)
• plexiglass box and plate with attached microphone
• earplug speaker
• Tektronix TDS 210 digital oscilloscope

2. Plug the microphone output bnc cable into the oscilloscope and with the microphone set at a corner of the box, tune the frequency and note the display. Can you see the resonances as you change the frequency? Describe what you see. Please be careful: the cable from the microphone to the preamp/bias box is short and fragile. Don't tug on it!

3. Make sure the microphone is connected to both the oscilloscope and the FFT spectrum analyzer. Turn on the analyzer in the usual way, by holding down the arrow key as you turn it on. Set up the SA in the following way: span to 12.5 kHz, press the measure key to get the measure menu on the screen, and select the display submenu. Change the display from log to linear - this will make your measurements easier. Again tune the frequency around, and describe what you see.

Question 1. Compare what you measure on the spectrum analyzer to what appears on the oscilloscope in the following way: Choose a frequency that gives you a relatively large signal on the oscilloscope and spectrum analyzer. Press the marker key and tune the knob on the SA to the peak, then read off the amplitude and frequency. Then use the cursors on the oscilloscope to measure the wave amplitude and frequency. How do these results compare? Explain what these two instruments, the SA and the o'scope, measure.

4. Now try to find the first six lowest frequency resonances of the box by tuning the frequency until you get a relatively large peak on the screen. As you use the arrow keys to increase the frequency, you will notice how the peak height on the SA display increases to a maximum. The frequency at such a relative maximum corresponds to a resonance, and is described by one of the standing wave patterns discussed in class. Continually adjust the span and start frequency settings to enable you to measure the frequencies with a relatively low span, say less than 1.5 kHz, so your frequencies will be relatively precise. The precision is determined by the fact that the horizontal scale is comprised of 400 discrete points, so the precision is essentially the span setting divided by 400. Note that you may have to tweak the frequency knob of the FG very carefully to maximize the peak height at each resonance. Also note that you may use the auto scale key to keep your signal on scale.

For each resonance, find the n_x and n_y values by sliding the appropriate edge of the box along the microphone and recording the number of nodes you observe. You could also check to see that the nodes create lines in the x-y plane by sliding the box such that a nodal line appears above the microphone. Each resonant frequency will be described by a set of three numbers, (n_x, n_y, n_z), each of which represents the number of nodes in the standing wave pattern as the box is slide along the respective direction, with the microphone just along the inside edge of the box.

Be sure to record room temperature so that you are able to calculate the speed of sound using the equation: v(m/s) = 331 m/s + 0.6 x T (C).

Analysis
Be sure to answer any questions asked in the procedure. Make a chart showing your six resonance frequencies, and the nodal assignments. Include a third column with the expected resonance frequencies based on the equation given above. To calculate these values, use the speed of sound based upon the room temperature and vary the node numbers, i.e., calculate (1,0,0), (0,1,0), etc. Comment on the agreement between experiment and theory.

Question 2. Do you see any modes that are harmonically related to other modes? Why or why not?

Question 3. Calculate what you'd expect the lowest frequency mode in the box to be if the box were filled with helium gas instead of air.

Question 4. What do you think you'd see on the spectrum analyzer if the earplug signal was not a single frequency, but a noise signal with equal intensity at all audio frequencies?

Return to Physics 104 homepage .